112專技高考公衛師

生物統計學

申論題

擬答
  • 沒有吃早餐的學童$X$上課精神不振比例 $ \hat{p_1} = \cfrac {64}{300}$
  • 有吃早餐的學童$X$上課精神不振比例$ \hat{p_2} = \cfrac {51}{400}$
  • 沒有吃早餐與有吃早餐的學童，上課精神不振比例差值的95%信賴區間為

    $ (\hat{p_1} - \hat{p_2} ) $ $ \pm Z_{0.025} \sqrt { \cfrac{ \hat{p_1} ( 1- \hat{p_1} )}{ n_1} + \cfrac{ \hat{p_2} ( 1- \hat{p_2} )}{ n_2} } $

    $ \Rightarrow ( \cfrac{64}{300} - \cfrac {51}{400} )$ $ \pm 1.96 \sqrt { \cfrac { \cfrac{64}{300} \times \cfrac{236}{300}}{300} + \cfrac { \cfrac{51}{400} \times \cfrac{349}{400}}{400} }$

    $ \Rightarrow [ 0.0291,0.1426 ]$

擬答

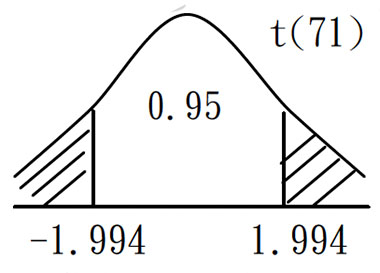
$ H_0:\mu =128 $
$ H_1:\mu \ne 128$
$ α=0.05$

$ T^*$ $ =\cfrac { \bar{X} - \mu_0 }{ S/ \sqrt{n}}$ $ = \cfrac{126.1-128}{15.2 / \sqrt{72}}$ $ -1.06 \notin C $

$C: \{ | T^* | > t_{0.975,71} = 1.994 \}$

不拒絕 $H_0$ ，沒有證據說該公司35歲到44歲的男性高階主管的平均血液收縮壓與該國男性平均收縮壓不同
擬答
  1. 在兩獨立母體變異數相同的情況下
    $ s_p^2 = \cfrac {(n-1) s_x^2 + (m-1) s_y^2 }{ n+m-2}$

    $ = 96.693$

    $t = \cfrac{ \bar{X} - \bar{Y} }{ \sqrt{ s_p^2 (\cfrac{1}{n} + \cfrac{1}{m}) }}$ $ = \cfrac{ 74-60 }{ \sqrt{ 95.693 (\cfrac{1}{10} + \cfrac{1}{10}) }}$

    $ = 3.200$
  2. 採用變異分析
    $ SST = \sum \sum (\bar{X}_{i．} - \bar{X}_{．．})^2 $ $ ＝\sum n_i (\bar{X}_{i．} - \bar{X}_{．．})^2 $

    $ 10 \times (60-67)^2 $ + $ 10 \times(74-67)^2 $ $=980$

    $ SSE = \sum \sum (\bar{X}_{ij} - \bar{X}_{i．})^2 $ $ = \sum (n-1)S_i^2 $

    $ = (10-1) \times 11.52^2 $ + $ (10-1) \times 7.66^2 $ $=1722.474 $

    ANOVA 表
     SSdfMSF
    組間980198010.241
    組內1722.4741895.693 
    總和2702.47419 
    所以 $F ＝ 10.241$
  3. $F ＝ 10.241$ ＝ $ t^2 = 3.200^2 $
    所以檢定兩組平均數是否相同，採用獨立樣本t檢定與ANOVA等價

選擇題

(B) 1某社區衛生局統計每日上午9：00至12：00，平均就診人數為10 人，請問 9月1日當天就診人數少於3人的機率為何？$（e^{-10} = 4.54×10^{-5}）$
  1. 0.0103
  2. 0.0028
  3. 0.0076
  4. 0.0023
(C) 2以下盒形圖（boxplot）來自世代研究調查資料，將資料中有中風者及無中風者的年齡以盒形圖繪製出其分布，利用此圖的訊息，對於中風與否之年齡分布描述，選出較合適的選項？
  1. 中風者之年齡分布呈現右偏分布，無中風者呈現左偏分布
  2. 中風者之年齡中位數小於無中風者
  3. 中風者之四分位距（interquartile range, IQR）大約為10歲，無中風者的年齡四分位距約為13歲
  4. 中風者之標準差（standard deviation）會大於無中風者
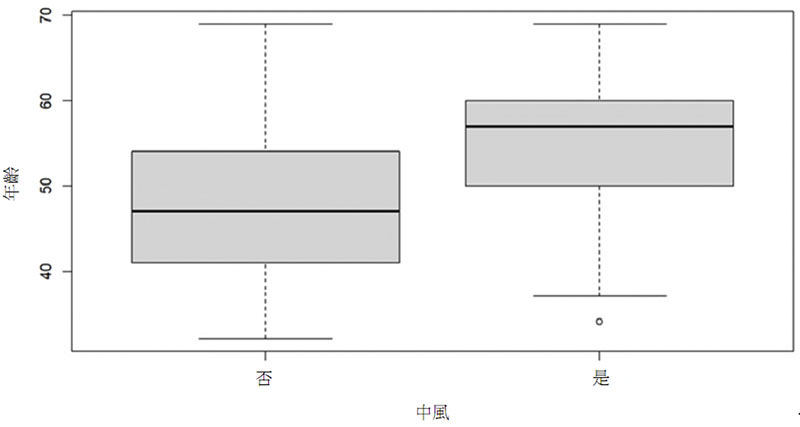
(D) 3在某大學新生體檢中，發現大學生健康狀況明顯較往年差，該校患有糖尿病的學生中男生之比例為0.7，該校沒有糖尿病學生中男生的比例為0.5，且年輕族群（18-20歲）糖尿病盛行率為1%，請問該校男學生中，患有糖尿病的比例為何？（四捨五入至小數第三位，選出最接近的答案）
  1. 0.011
  2. 0.010
  3. 0.016
  4. 0.014
(A) 4某大學大一統計成績服從常態分配，平均數為78分，標準差為5，共有500位修習統計學，請問有一位同學分數為88分，請問其排名為何？PR 值為何？（選出最接近選項）
  1. 排名約為第13名、PR 值約為97.5
  2. 排名約為第25名、PR 值約為95
  3. 排名約為第5名、PR 值約為99
  4. 排名約為第50名、PR 值約為90
(B) 5在流行病學研究中，常利用性別及年齡配對，來了解暴露及疾病之相關性。以下資料為世代研究（cohort study）收集而來，想了解抽菸對於肺癌之影響，以不同條件暴露狀況進行性別及年齡配對，以一位有抽菸者和一位未抽菸者進行性別及年齡的配對，再觀察兩人是否有罹患肺癌，並檢定抽菸和肺癌之相關性。請針對此資料的檢定結果，選出正確的選項。（檢定時皆不進行連續型修正）
 有抽菸者
無抽菸者肺癌無肺癌
肺癌123（A）220（C）
無肺癌260（B）150（D）
  1. 在此研究設計所得資料，可利用費雪精確檢定進行了解
  2. 若運用正確的檢定方法下，此檢定的檢定統計量應為3.33
  3. 在此研究設計所得資料，並製作成上表，表中所呈現的人數共有753人
  4. 在顯著水準為0.05下，我們拒絕虛無假設，證實抽菸和肺癌間具有相關性
(D) 6想了解戴口罩對於預防新冠肺炎是否有效益，共收集 100 人，進行回顧式研究，其中有得病及未得病者，分別各有 50人，請他們回顧過去一個月戴口罩之狀況，資料如下，下列描述何者錯誤？
 戴口罩頻率高K=0戴口罩頻率低K=1總合
此星期曾感染新冠肺炎D=128（a）2250
此星期未曾感染過新冠肺炎D=0331750
  1. 有符合卡方之假設，故可使用卡方檢定進行分析
  2. 若要計算格子之期望個數，格子（a）之期望個數為30.5
  3. 若利用勝算比（odds ratio）之估計及檢定進行此問題之探討，戴口罩頻率低者染病風險大約是戴口罩頻率高者的1.53倍，但不具統計上之顯著
  4. 若利用勝算比估計及檢定兩者之相關性，勝算比估計值之標準誤可利用 { $ \sqrt{1/22}$ +$ \sqrt{1/28}$ +$ \sqrt{1/33}$ +$ \sqrt{1/17}$ }估計之
(B) 7研究顯示慢跑及快走皆是有益身心之運動，國外研究顯示在既定的公里數下，慢跑所需熱量較快走多，在此收集以下資料，想驗證此結果；在進行相同的公里數下（1.6公里）所需消耗之熱量如下（單位：大卡）：
參與者12345
跑步113115110105150
快走8880908592
共有10個年齡相仿之參與者，隨機分派兩組，下列描述何者正確？
  1. 可使用兩組獨立平均數檢定，為檢定兩組平均數之方法
  2. 使用Wilcoxon rank sum 檢定方法，為檢定兩組中位數之方法
  3. 使用Wilcoxon signed-rank檢定方法，為檢定兩組中位數之方法
  4. 使用McNemar 檢定方法，為檢定兩組成對中位數之方法
(A) 8研究者欲瞭解具有某項飲食習慣的有無，是否會導致某疾病的發生，他將研究資料整理如下：
具有該項飲食習慣、但沒有罹病：400 人
具有該項飲食習慣、也有罹病：100 人
不具該項飲食習慣、也沒有罹病：200 人
不具該項飲食習慣、但有罹病：300 人
若研究者將上述資料置入 logistic regression 中，則可計算出，具有該項飲食習慣者罹病之Crude Odds Ratio 為何？
  1. 0.17
  2. 0.50
  3. 2.00
  4. 6.00
(B) 9若針對宜蘭地區居民進行腰圍之測量，抽出 500 位居民（無遺失值） ，其樣本腰圍平均數為78.89公分、樣本腰圍標準差為9.72 公分。男性為250人，其樣本腰圍平均數為83.07公分、標準差為9.99公分；女性為250人，其樣本腰圍平均數為74.70公分、標準差為9.67公分。下列何者正確？
  1. 在比較男性、女性之腰圍平均是否有差異時，可使用成對樣本平均數（paired t test）檢定
  2. 若要利用此資料建構宜蘭地區居民腰圍平均值的 95%信賴區間，其信賴區間約為（78.04, 79.74）
  3. 男性腰圍大於 90 公分定義為肥胖，若要檢定此地區男性居民平均腰圍是否大於 90 分，以此資料可得，在顯著水準為0.05時，可以證明此地區是男性居民平均腰圍大於90公分
  4. 在顯著水準為0.05時，此地區男性平均腰圍和女性平均腰圍無法證明兩者間具有顯著差異
(A) 10最近研究發現＂人工甜味劑「阿斯巴甜」可能對人類致癌＂，一般食品的規範中，食品每100公克含糖量不超過0.5公克，即可宣稱「無糖」 ，這些宣稱無糖的食品，卻添加了許多人工甜味劑，長期而言，非全然對健康無害。若要想檢測此食品是否可宣稱「無糖」，我們抽出數個樣本進行檢測，測量每100公克的含糖量，以下對於虛無假設及對立假設的設定，何者正確？
  1. $H_0:\mu \le 0.5$ vs $H_1:\mu > 0.5$
  2. $H_0:\mu = 0.5$ vs $H_1:\mu \ne 0.5$
  3. $H_0:\mu ＜ 0.5$ vs $H_1:\mu \ge 0.5$
  4. $H_0:\mu \ge 0.5$ vs $H_1:\mu ＜ 0.5$
(C) 11我們可以利用中央極限定理的結果，建構$\mu $的95%信賴區間，稱為（a, b） ，針對此信賴區間的描述，何者正確？
  1. 表示$\mu $有95%的機率會在（a, b）之間
  2. 表示此（a, b）必會包含 $\mu$
  3. （a, b）區間愈長表示標準誤愈大，代表樣本數較小
  4. 建置$\mu $的95%信賴區間，會比99%信賴區間來得長
(C) 12在心血管疾病的研究中，腰圍為重要的影響因子，控制腰圍大小為預防心血管疾病管道之一，我們想了解腰圍大小（Y）和收縮壓（X）之相關性。利用簡單線性迴歸模型$ \mu_{Y|X} = α + \beta X $或皮爾森（Pearson）相關係數（$\rho $）了解兩者間之相關性，下面描述何者錯誤？（假設腰圍、收縮壓為常態分配）
  1. 簡單線性迴歸模型或皮爾森相關係數，皆是可以了解腰圍大小和收縮壓之直線相關的程度
  2. 若腰圍大小（Y）和收縮壓（X）皆進行標準化後，分別為 $ y^\prime $及$ x^\prime $，再進行線性迴歸模型，可得$ \mu_{ y^\prime | x^\prime }= α^\prime + \beta^ \prime x^\prime $模型，其$ \beta \prime $的估計值會很接近 $\rho $ 的估計值
  3. 線性迴歸模型中的斜率（$ \beta $）可描述腰圍大小和收縮壓兩者互相影響之變化程度，若$ \beta $愈大表示兩者相關性愈大
  4. 若皮爾森相關係數或線性迴歸之斜率（$ \beta $ ）為0，腰圍大小和收縮壓間，有可能為曲線相關，也有可能是無相關性
(B) 13在治療自體免疫性疾病的藥物中，除了非類固醇抗發炎藥（NSAID）外，還有免疫抑制劑的選擇。以下資料來自 200 位疾病嚴重度相似的自體免疫性疾病患者，有 100 位接受 Drug 治療（Drug=0，為參考組），有100位接受免疫抑制劑的治療（Drug=1），觀察治療半年後疾病狀況是否有改善（Y=1：有改善；Y=0：無改善），在調整年齡（Age）、性別（Gender=0，女性（參考組）；Gender=1，男性）後，下列式子及下表為多變項模型及其估計結果（顯著水準為0.05）。下列描述何者正確？
logit={Pr(Y=1 | $Drug$,$Gender$,$Age $)} $ = α+ \beta_1 \times Drug$ + $\beta_2 \times Gender$ + $\beta_3 \times Age$
 EstimateStd. Errort value
Drug ($\hat{\beta_1}$)0.30480.06904.421
Gender ($\hat{\beta_2}$)0.46860.06397.3 5
Age ($\hat{\beta_3}$)-0.00280.0017-1.642
  1. 在此模型中，可判斷年齡及性別為干擾因子
  2. 在模型估計結果中，調整年齡（Age）及性別（Gender）下，在治療半年後，使用免疫抑制劑藥物會較使用NSAID病況有改善，且有統計上之顯著
  3. 在控制其他變數下，在治療半年後，男生較女生病況有改善，但無統計上顯著
  4. 在控制其他變數下，在治療半年後，年齡愈小病況有改善的可能性較高，且有統計上顯著
(A) 14在心血管疾病的研究中，腰圍為重要的影響因子，控制腰圍大小為預防心血管疾病管道之一，我們想了解腰圍大小（$Y$）和收縮壓（$X_1$）之相關性，並考慮調整年齡（$X_2$）及性別（$X_3$） ，男性為1，女性為0，女性為參考組）。以下利用簡單線性迴歸及複迴歸模型，探討腰圍和收縮壓之相關性，請計算模型三中$\beta_1$之95%信賴區間估計。（此資料樣本數為5019，遺失值變數最多為3%，顯著水準為0.05）
模型一$ \mu_{Y|X_1} $ $= α + \beta_1 X_1 $
模型二$ \mu_{Y|X_1,X_2,X_3} $ $= α + \beta_1 X_1 + \beta_2 X_2 $
模型三$ \mu_{Y|X_1,X_2,X_3} $ $= α + \beta_1 X_1 + \beta_2 X_2 + \beta_3 X_3 $
模型四$ \mu_{Y|X_1,X_2,X_3} $ $= α + \beta_1 X_1 + \beta_2 X_2 + \beta_2 X_3 $ $+ \beta_4 (X_1 \times X_3)$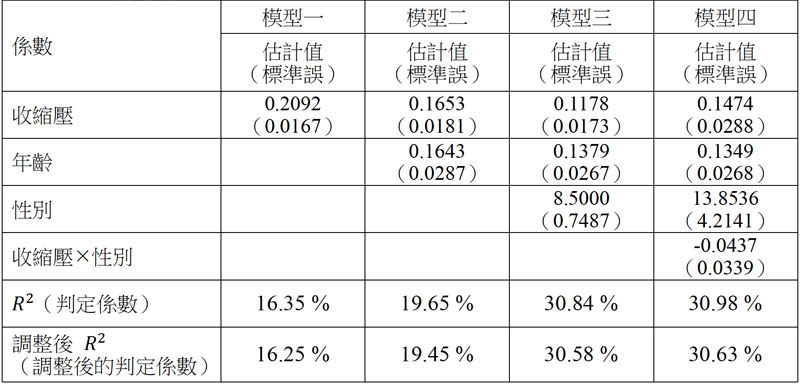
  1. 模型三中$\beta_1$之95%信賴區間估計為(0.08, 0.15)
  2. 模型三中$\beta_1$之95%信賴區間估計為(0.18, 0.24)
  3. 模型三中$\beta_1$之95%信賴區間估計為(0.09, 0.20)
  4. 模型三中$\beta_1$之95%信賴區間估計為(0.08, 0.19)
(B) 15承上題，對於模型一、二、三、四之描述，何者錯誤？
  1. 在這四個模型中，以模型選擇的概念（估計參數個數最少、解釋力最大），若要選一個較佳的模型，應該選擇模型三最合適
  2. 模型二中，其調整後的$R^2$= 19.45%，表示年齡及收縮壓可解釋腰圍的總變異佔19.45%
  3. 模型一中，可推得腰圍和收縮壓的皮爾森（Pearson）相關係數為0.404
  4. 在模型四中，顯示交互作用不存在，表示腰圍和收縮壓之間的相關，不受年齡之不同而改變定
(A) 16肺癌發生率為每十萬人口36 人，為臺灣前10 大癌症之一，以下為某醫學中心，肺癌存活率之資料(以月為單位)，是利用Kaplan-Meier 估計方法得到，gender=0 為女性，gender=1 為男性，在曲線上"+＂為設限（censor），以下描述何者錯誤？
  1. Kaplan-Meier估計方法，需在兩條存活曲線沒有相交的狀況下進行估計
  2. 此Kaplan-Meier估計結果中，存活中位數，男性為40個月，女性為70個月
  3. 曲線有下降表示有因肺癌死亡之事件發生
  4. 第 80 個月後曲線為平行線，表示在第 80 個月後，無個案因肺癌死亡，但有幾個個案是非因肺癌死亡
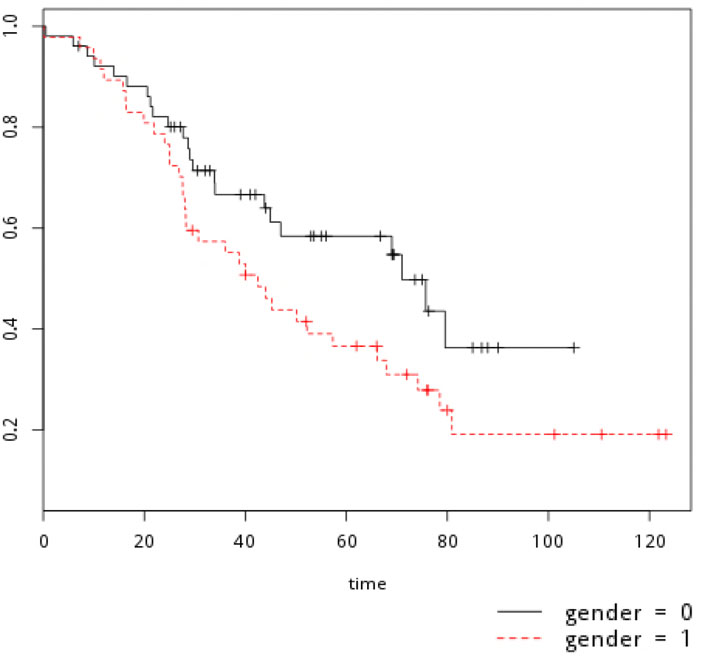
(D) 17承上題，我們想了解男性、女性之存活曲線是否有差異，利用以下方法進行檢定，請問以下描述，何者正確？（顯著水準為0.05）
檢定方法檢定統計量p-value
Log-Rank 檢定3.55620.0593
Peto-Wilcoxon 檢定2.81820.0932
  1. Log-Rank 檢定，需假設兩條 log-存活函數的比值需為常數（風險比為常數），故非為無母數（nonparametric）檢定
  2. 此兩條存活函數在後期差異較大，使用Peto-Wilcoxon 檢定進行兩組存活曲線比較時，其檢定力較好
  3. 以 Log-Rank檢定或 Peto-Wilcoxon 檢定之p-value，有充份證據證明男性、女性存活曲線是有顯著差異
  4. Log-Rank檢定或Peto-Wilcoxon檢定方法，其抽樣分配為自由度為1之卡方分配
(A) 18我們利用 Cox PH model(Cox proportional hazard model)進行影響因肺癌死亡之風險因子的探討，以因肺癌死亡為事件發生，並記錄從追踪到因肺癌死亡發生之時間，模型之解釋變項為性別（男性、女性，女性為參考組）、年齡、抽菸程度（從未抽菸、過去曾抽菸現在無抽菸、現在有抽菸，現在有抽菸為參考組），依據以下分析結果，那些為影響存活之因子，請選出正確選項：
  1. 年齡為唯一顯著之影響存活之變數
  2. 性別、年齡、抽菸與否，皆為顯著影響存活的變數
  3. 性別、抽菸與否，為顯著影響存活的變數
  4. 上述未呈現p-value，故無法判斷何者為顯著影響存活的變數
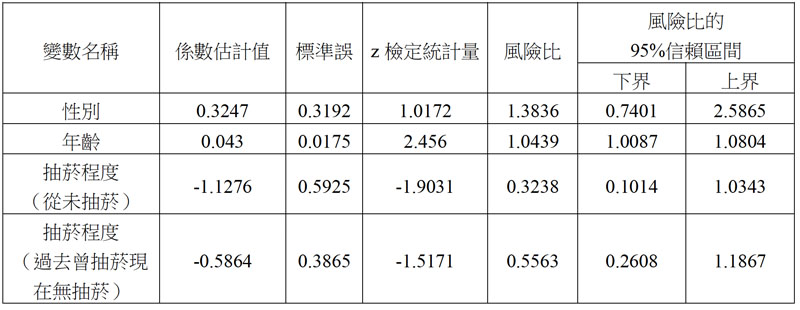
(B) 19承上題，依據上題分析結果，對於模型參數之解釋何者正確？
  1. 在控制其他變數下，男性發生因肺癌死亡的機率是女性的1.38倍
  2. 在控制其他變數下，從未抽菸者發生因肺癌死亡的風險是現在有抽菸者的0.32倍
  3. 在控制其他變數下，年齡每增加一歲，發生因肺癌死亡的風險會增加104%
  4. 在控制其他變數下，現在有抽菸者發生因肺癌死亡的風險是過去曾抽菸現在無抽菸者的0.56倍
(B) 20在一個Mean=Median=Mode的常態分布中，加入若干個極大值後，請問下列敘述何者正確？（假設仍然只有一個Mode）
  1. Median一定變大、Mode一定不變
  2. Median可能變大或是不變、Mode可能變大或是不變
  3. Median一定變大、Mode可能變大或是不變
  4. Median可能變大或是不變、Mode一定不變
(A) 21在盒型圖（boxplot）中，圖形中央四邊形所對應的數值範圍，涵蓋了這個變數多少比例的觀察值？（α為顯著水準）
  1. 50%
  2. 75%
  3. 95%
  4. 100(1-α)%
(C) 22在執行完「變異數分析」的檢定之後，碰到下面那種情況時，需要再進行「事後檢定」（或稱「多重比較」）？
  1. 各組的變異數不相等
  2. 各組的中位數不相等
  3. 各組的平均數不相等
  4. 各組的峰度和偏態不相等
(D) 23在《莊子．齊物論》有一則寓言：養猴人跟猴子們說，以後早上餵三升橡實，下午餵四升橡實，但猴子們聽了很不高興，因為早上吃太少，於是，養猴人說，那改成早上餵四升，下午餵三升，猴子們就很高興（此即朝三暮四的典故）。假設養猴人對這些猴子進行這兩種餵食方式的滿意度調查，結果如下（a,b,c,d為猴子的個數）：
 朝四暮三
朝三暮四滿意不滿意
滿意ab
不滿意cd
試問，養猴人該用 何種方法來進行統計檢定？
  1. Test of goodness-of-fit
  2. Test of independence
  3. Fisher's exact test
  4. McNemar's test
(A) 24將某兩個變數置入simple linear regression後，得到其決定係數為0.64，若將這兩個變數進行相關分析，則其相關係數應為下列何者？
  1. $0.64^{0.5}$
  2. $0.64^1$
  3. $0.64^2$
  4. 條件不足無法計算
(B) 25某研究者收集了 10 名罕見疾病患者的發病年齡，若欲比較男性和女性之發病年齡是否有差異，則該使用何種統計方法來進行檢定？
  1. Kruskal-wallis test
  2. Wilcoxon rank-sum test
  3. Wilcoxon sign-ranked test
  4. Spearman correlation
(C) 26在下列四種統計檢定方法中，共有幾種方法可以對自變數進行調整 （adjustment，或稱控制）？
①Simple linear regression
②Logistic regression
③General linear model
④Cox proportional hazard model
  1. 1種
  2. 2種
  3. 3種
  4. 4種
(B) 27Kruskal-Wallis test 的虛無假設為下列何者？
  1. 各組資料母群體的平均數相等
  2. 各組資料母群體的中位數相等
  3. 各組資料母群體的眾數相等
  4. 各組資料母群體的變異數相等
(D) 28在使用統計軟體進行性別、血型、身高（以上三項為自變數）對於體重（依變數）的複迴歸分析時，如果在報表中有出現一項下表中的結果：
參數估計值p-value
[性別=女] * [血型=A]ab
則代表有對這兩個變數進行下列何種探討？
  1. 加權效果
  2. 加乘作用
  3. 聯合效應
  4. 交互作用
(B) 29在某次選舉中，研究者對三位候選人進行支持度的民意調查，結果發現，甲、乙、丙三位候選人的支持度分別為30%、27%、20%。試問：該研究者還需要下列那一種指標，才能判斷候選人之間的支持度是不分軒輊，或是具有統計上的顯著差異？
  1. 已經可以直接判定，不需其它指標
  2. 各候選人支持度的信賴區間
  3. 各候選人支持度的標準差
  4. 各候選人支持度的檢定力（power）
(D) 30在實務研究上，若發現欲對一個2×3列聯表進行檢定時，其中有兩個細格（cell）的期望值不符合Pearson's chi-square test的使用前提。試問：在進行下列那一項動作之後，就能夠有機會且合理地使用該檢定方法？
  1. 將橫列的組別合併
  2. 將直行最少個數的組別與次少個數的組別合併
  3. 將直行最少個數的組別與最多個數的組別合併
  4. 增加樣本數1
(B) 31有一檢測之陽性預測值為60%，令其敏感度為100%，可得之陰性預測值為何？
  1. 60%
  2. 100%
  3. 90%
  4. 80%
(C) 32承上題，令其特異度為33%及群體得病率為50%，請問檢測陽性者為得病之條件機率為何？
P (D+|T+) = P (D+)*sensitivity/ (P (D+)*sensitivity+ (1-P (D))*(1-specificity))
  1. 30%
  2. 50%
  3. 60%
  4. 90%
(D) 33下列四種資料尺度中，那一種的等級（或稱數值化程度）是最低的？
  1. Ratio scale
  2. Interval scale
  3. Ordinal scale
  4. Nominal scale
有一多中心體外反搏介入研究（MUST-EECP），其中 71 人為個案組，66 人為對照組，其心絞痛年平均值（標準差）分別為8.56(7.88)對4.5(4.06)。請回答第34題至第36題：
(A) 34請問其標準誤分別為何？ 標準誤=標準差 / $ \sqrt{樣本大小}$
  1. 0.94對0.50
  2. 0.50對0.94
  3. 7.88對4.06
  4. 4.06對7.88
(B) 35請問個案組vs 對照組心絞痛年95%信賴區間下限vs上限分別為何？
95%信賴區間=平均值±1.96×標準誤
  1. 10.39 vs 5.48
  2. 6.73 vs 5.48
  3. 10.39 vs 3.52
  4. 6.73 vs 3.52
(A) 36請問個案組與對照組二組心絞痛年平均值之差異應用何種統計方法檢定？
  1. Student's t-test
  2. Paired t-test
  3. Chi-square test
  4. McNemar test
(C) 37如表，設定的顯著性水平（通常為0.05），請問下列敘述何者最不適當？
Logistic model predictionActual measurementMcNemarCorrelation coefficient
FailPassP valueSpearmanP value
Fail39(40.63)13(13.54).84.477<.001
Pass12(12.50)32(33.33)---
  1. McNemar test 未達統計顯著
  2. 推論預測與實測結果未達統計顯著差異
  3. 推論預測與實測關聯未達統計顯著關聯
  4. Spearman correlation coefficient 為0.477 (p < 0.001)達統計顯著
(D) 38承上題，請問下列敘述何者最不適當？
  1. Chi-square test 用以檢定獨立樣本
  2. McNemar test 用以檢定相依樣本
  3. Spearman correlation用於評估兩個變數之間的相關性，特別是在變數之間存在非線性關係時
  4. 相關係數的取值範圍在-1到1之間，-1表無關，1表有關
(C) 39想針對臺灣四個地區（北、中、南、東）進行 BMI 之調查，是否不同區域之 BMI 之平均數會有差異，以下為 ANOVA 的分析結果，資料無遺失值。在顯著水準為 0.05 時，針對下表ANOVA的結果，選出正確選項？ 說明：$Pr(F>F_{(p,3,4823)})$$=p,F_{(p,3,4823)}$為$(1-p)$th百分數 $ F_{0.05,2,4824} = 2.9976 $， $ F_{0.05,3,4823} = 2.6068 $， $ F_{0.05,4,4822} = 2.3738 $， $ F_{0.05,5,4821} = 2.2160 $， $ F_{0.05,4824,2} = 19.4955$， $ F_{0.05,4823,3} = 8.5270$， $ F_{0.05,4822,4} = 5.628824$， $ F_{0.05,4821,5} = 4.3658$
變異來源平方和自由度平均平方和F值
處理130.40(B)(D)(F)
誤差(A)(C)(E) 
總和97996.894826 
  1. 格子中(B)及(C)中，為描述ANOVA檢定之抽樣分配的自由度，其值分別為(B)＝4822、(C)＝4
  2. 從ANOVA表中，在資料無遺失的狀況下，可推得此研究的樣本數共有4826筆
  3. 依ANOVA的假設之一，每地區的BMI資料變異數都相同，故我們可以利用ANOVA表中的數值來估計母體的變異數，其母體變異數估計值約為20.30
  4. ANOVA檢定之抽樣分配為F分配，由此結果得知是拒絕虛無假設，在顯著水準為0.05時，有證據顯示此四地區之BMI平均數不全相等
(C) 40承上題，所採取的檢定方式，其虛無假設及對立假設為何？
  1. $H_0:\mu_北 =\mu_中 =\mu_南 =\mu_東 $ 全部相等 vs $ H_1: \mu_北 \ne \mu_中 \ne \mu_南 \ne \mu_東 $ 全不相等
  2. $H_0:\mu_北 \ne \mu_中 \ne \mu_南 \ne \mu_東 $ 全不相等 vs $ H_1: \mu_北 =\mu_中 =\mu_南 =\mu_東 $ 全部相等
  3. $H_0:\mu_北 =\mu_中 =\mu_南 =\mu_東 $ 全部相等 vs $ H_1: \mu_北、\mu_中、\mu_南、\mu_東 $ 不全相等
  4. $H_0:\mu_北 、\mu_中 、\mu_南 、\mu_東 $ 不全相等 vs $ H_1: \mu_北 =\mu_中 =\mu_南 =\mu_東 $ 全部相等

※本站所有內容皆為志光教育科技集團版權所有，未經同意請勿任意複製、轉載、發行或刊他處。

▲
TOP