111地特三等衛生行政.衛生技術

生物統計學

申論題

擬答
《考題難易》：★
《解題關鍵》：非常基本的考題，樣本平均數機率的運算，但須留意題目所提供的資訊是標準誤而非標準差，並且也需要留意考卷提供的是常態分配左半表。相關考題可參閱111年高考衛行、110年薦任與108年薦任試題。
《命中特區》：生物統計學課本p104；生物統計學精選500題全解p93～94。
假設每天熱量攝取為$X$
$P(\bar{X} \le 1560)$ $ = P(Z \le \cfrac{1560-1579.71}{39.61}) $ $ = P(Z \le -0.50)$ $= 0.3085 $
擬答
《考題難易》：★
《解題關鍵》：獨立樣本t檢定為課內基本考題，幾乎每年都會出題，相信可以輕鬆拿分。
《命中特區》：生物統計學課本p164～172；生物統計學精選500題全解p185～196。
假設男性血漿維生素B6為X
女性血漿維生素B6為Y
$H_0 ：\mu_x = \mu_y $
$H_1 ：\mu_x \neq \mu_y $
$a=0.05$

$s_p^2 = \cfrac {(b-1)s_x^2 + (m-1)s_y^2}{n+m-2} $

$ =\cfrac {(36-1)・10.86^2 + (36-1)・10.02^2}{36+36-2} $
$ =\frac {(36-1)・10.86^2 + (36-1)・10.02^2}{36+36-2} $
$= 109.17$

$ T^* = \cfrac {\bar{X} - \bar{Y} }{ \sqrt{ s_p^2 \left( \cfrac{1}{n} + \cfrac {1}{m} \right)} } $ $= \cfrac {20.1-18.6}{ \sqrt{ 109.17 \left( \cfrac{1}{36} + \cfrac {1}{36} \right)} }$ $= 0.609 \notin C $

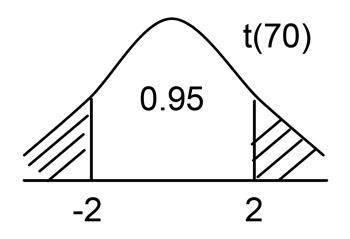$C:\{ |T^*| > t_{0.025} (70) \thickapprox 2\} $

不拒絕$H_0$ ，沒有顯著的證據說
男性及女性的血漿維生素B6有差異
註:本卷未附合適的t分配查表值，所以採用大樣本Z檢定亦可。
擬答
考題難易》：★
《解題關鍵》：
單母體比例值之信賴區間雖屬課內基本題，但過去的命題率較低，可參考105年地特三等衛生與102年高考衛生相同考法。《命中特區》：生物統計學課本p127～128；生物統計學精選500題全解p185～196
設高職青少女發生性行為率為$p$
$ \widehat{p} = \cfrac{432}{3600}=0.12 $
高職青少女發生性行為率 $p$之95%信賴區間為
$\widehat{p} \pm Z_{0.025} \ \sqrt{ \cfrac {\widehat{p}(1-\widehat{p})}{n} } $

$\Rightarrow 0.12 \pm 1.96 ・ \sqrt{ \cfrac{0.12 \times 0.88 }{3600}}$

$\Rightarrow \left[ 0.1094, 0.1306 \right] $
擬答
《考題難易》：★
《解題關鍵》：課內已強調迴歸分析屬考試基本必出題，本題難度並不高，迴歸係數計算、變異數分析表以及迴歸係數與判定係數的解釋本就是必考題，應可完整拿下分數。近年有許多類似考題，111年高考即有非常相似的考題。
《命中特區》：生物統計學精選500題全解p頁379～380、p390～394
  1. 變異數分析表整理如下
    SourceDFSum of
    Squares    		Mean
    Square    		F ValuePr > F
    Model16.686.6811.83＜0.01
    Error396223.60.5646  
    Total397230.28  
    變異數分析表可用以檢定迴歸模式是否成立

    $ H_0：b =0 $
    $ H_1：b \ne 0$
    假設 $ a = 0.05 $
    $ F^* = 11.83 $ ，對應之 $ p-value < 0.01 < a = 0.05 $
    拒絕$H_0$ ，代表迴歸直線有達到統計上的顯著性
  2. 判定係數 $ R^2 = \cfrac {SSR}{SSTO} \times 100\% $ $ = \cfrac {6.68}{230.28 } = 2.9\%$
    此簡單線性迴歸模式對實習壓力解釋度為2.9%
  3. 此處假設因應分數愈大實習壓力分數也愈大
    所以因應分數與實習壓力分數相關係數為$ r_{x,y} $ $ = + \sqrt{ \cfrac { 6.68}{ 230.28} } = 0.1703 $

    $ b $ $ = r_{x,y} \cfrac {S_Y}{S_X}$ $ = 0.1703 \times \cfrac {0.76}{ 0.6} $ $ = 0.2157 $

    $ a $ $ = \bar{Y} - b \bar{X} $ $ = 1.56 - 0.2157 \times 1.59 $ =$ 0.1217$
  4. 預測迴歸方程式為$ \hat{Y} = 1.217 + 0.2157X $
    $ X=3 $，實習壓力分數預期值為 $ \hat{Y} = 1.217 + 0.2157 \times 3 $ $= 1.8641$

※本站所有內容皆為志光教育科技集團版權所有，未經同意請勿任意複製、轉載、發行或刊他處。

▲
TOP