111高考衛生技術

生物統計學(含流行病學)

申論題

擬答
考題難易：★★☆☆☆
解題關鍵：雖然盒鬚圖與對應的離群值判斷是課內基本內容，但過去國考未曾命題過，可能會有所猶豫，但仍是基本可以得分的題目。
可參考王瑋，生物統計學P.27與P.36例題說明。
  1. 將CT值重新排序如下：
    2, 5, 7, 9, 10, 11, 12, 12, 12, 13, 13, 13,
    14, 15, 16, 16, 17, 17, 17, 18, 18, 32, 40, 139
    1. 由圖可知非離群值的最大值為18
    2. $ Q_3$ = $ \cfrac {X_{(18)} + X_{(19)} }{2}$ = $ \cfrac {17+17}{2}$ $=17$
    3. $ Q_1$ = $ \cfrac {X_{(6)} + X_{(7)} }{2}$ = $ \cfrac {11+12}{2}$ $=11.5$
    4. 由圖可知非離群值的小值為5
  2. $IQR = $ Q_3 - Q_1 $ = 17-11.5 = 5.5$
    界外值的上限為
    $ Q_3 + 1.5IQR $ = 17 + 1.5 × 5.5 = 25.25
    界外值的下限為
    $ Q_1 - 1.5IQR $ = 11.5 - 1.5 × 5.5 = 2.75
擬答
考題難易：★★☆☆☆
解題關鍵：雖然盒鬚圖與對應的離群值判斷是課內基本內容，但過去國考未曾命題過，可能會有所猶豫，但仍是基本可以得分的題目。
可參考王瑋，生物統計學P.27與P.36例題說明。

  1. 設A方案腫瘤細胞體積為$X_i$，B方案腫瘤細胞體積為$Y_i$
    $ SE_x $ $= \cfrac {S_x}{\sqrt{n}} \Rightarrow S_x $ $= 0.7 \times \sqrt{13} $ $= 2.5239 $

    $ SE_y $ $= \cfrac {S_y}{\sqrt{m}} \Rightarrow S_y $ $= 0.83 \times \sqrt{25} $ $= 4.15 $

    $H_0:\sigma _x^2 = \sigma _y^2$
    $H_1:\sigma _x^2 \ne \sigma _y^2$

    $ a=0.05 $

    $F^*$ = $\cfrac {S_y^2}{S_x^2}$ = $\cfrac {4.15^2}{2.5239^2}$ = $2.70 \notin C $

    不拒絕 $H_0$，所以沒有顯著證據說變異數不相同


  2. $ H_0 : \mu_x=\mu_y $
    $ H_1 : \mu_x \ne \mu_y $
    $ a=0.05 $

    $ s_p^2 $ $= \cfrac {(n-1)s_x^2 + (m-1)s_y^2}{ n+m-2}$ $= \cfrac {12・2.539^2 + 24・4.15^2 }{ 12+24}$ $= 13.6050 $

    $ T^* =$ $ \cfrac { \overline{X}-\overline{Y}}{ \sqrt {s_p^2 \left( \cfrac{1}{n}+\cfrac{1}{m} \right) } }$ $= \cfrac {6.4-5.2}{ \sqrt {13.605 \left( \cfrac{1}{13}+\cfrac{1}{25} \right)}}$ $ = 0.95 \in C $

    $ C:\{ |T^*|>t_{.36,0.975}=2.028 \} $
    不拒絕$H_0$ ，沒有顯著的證據說
    A與B方案對腫瘤細胞體積的治療效果不相等
擬答
考題難易：★★☆☆☆
解題關鍵：
本題算是很巧妙的期望同學可以將屬量資料轉屬質的二分類形式，觀念相當單純，但因為過去也未曾考過，也會具有相當鑑別度。本題比較疑慮的是期望次數很小，也可以採用費雪精確檢定。卡方檢定齊一性檢定則可參考王瑋，生物統計學P.255至P.262諸多類似試題，費雪精確檢定則可參考王瑋，生物統計學P.264相同範例。
  1. $\overline{X} =\cfrac {12+10+...+33}{12} =19.9167 $

    A樣本變異數
    $ S^2$ $ = \cfrac {\sum_{i=1}^N (X_i - \overline{X} )^2 }{n-1}$ $ =\cfrac {(12-19.9167)^2 +...+(33-19.9167)^2}{12-1}$ $=296.6288$

    排序B 樣本 8, 11, 12, 14, 14, 18, 18, 22, 22, 23, 55, 59, 67, 68
    第一四分位數為 $Q_1 = X_{(4)} = 14$
    第三四分位數為 $Q_3 = X_{(11)} = 55$
    四分位差 $ QD = \cfrac {Q_3 -Q_1}{2} $ = $\cfrac {55-14}{2}$ $=20.5$
  2. DEHP以50為切點，分為是否過量暴露，資料重新整理如下，並且計算各格子的期望值，斜線的左上方為觀察值，右下角為期望值

    $ a=0.05$，$df=(2-1)\times (2-1)=1$

    以Yate’s校正後計算檢定統計量

    $ X^{2^*}$ $= \sum \cfrac {(|O_i - E_i |- \frac {1}{2})^2 }{E_i}$ $= \cfrac {(|1 - 2.31 |- 0.5)^2 }{2.31}$ + ...+ $ \cfrac {(|10 - 11.31 |- 0.5)^2 }{11.31} $ $ = 0.65 \notin C$


    不拒絕$H_0$，沒有顯著證據說兩個群體DEHP的比例不相等
    註：有50%格子的期望次數小於5，所以應該採用Fisher’s exact檢定
    Step 1.
     過量無過量總和
    A11112
    B41014
    總和52126

    $ \cfrac {12! \times 14! \times 5! \times 21!}{26! \times 1! \times 11! \times 4! \times 10!} = 0.1826 $

    Step 2.
     過量無過量總和
    A01212
    B5914
    總和52126

    $ \cfrac {12! \times 14! \times 5! \times 21!}{26! \times 0! \times 12! \times 5! \times 9!} = 0..0304 $

    Step 3.
    得$p - value$ $=0.1826 + 0.0304$ $ =0.2130 > a $
    不拒絕$H_0$ ，沒有顯著證據說兩個群體DEHP的比例不相等
擬答
考題難易：★★☆☆☆
解題關鍵：出題想法非常不錯，只可惜題目少給了三種快篩劑的受檢數，導致此題的結果不會一致。
卡方檢定與勝算比的信賴區間再流病考卷中也算是常見命題，可參考109年地特四等衛政考題，另外99年地特三等衛政型式亦與本題類似，可參考王瑋，流行病學P.6-21與P.6-24命中試題。
  1. 偽陰率=1－敏感度
    A快篩劑偽陰率為 1-0.88=0.12
    C快篩劑偽陰率為 1-0.86=0.14
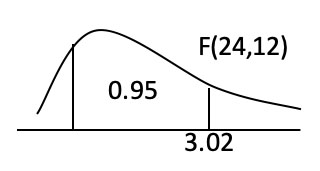
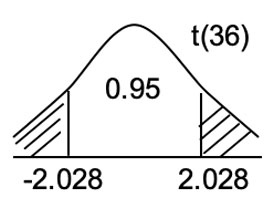
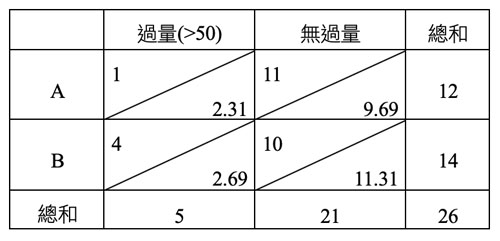
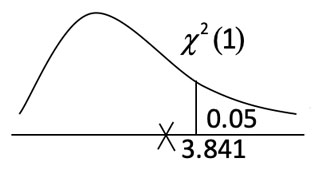
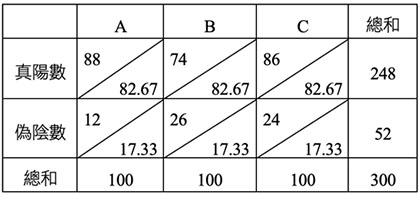  2. 假設A、B、C快篩劑皆有100位受試者，可將資料整理如下，並且計算各格子的期望值，斜線的左上方為觀察值，右下角為期望值 $ a=0.05$，$df=(3-1)\times (2-1) =2$

    $ X^{2^*}$ $= \sum \cfrac {(O_i - E_i)^2 }{E_i}$ $=\cfrac {(88-82.67)^2 }{82.67}$ + ...+ $ \cfrac {(24-17.33)^2 }{17.33} $ $ = 8 \notin C$


    拒絕$H_0$，有顯著證據說三種快篩劑偽陰率不相等
  3. 延續(二)，
    $ OR = \cfrac {86 \times 26 }{ 74 \times 24} = 1.26$

    $ ln(OR)=0.2303 $，$ \sqrt{ \cfrac{1}{74}+ \cfrac{1}{86} + \cfrac{1}{26} + \cfrac{1}{24}} = 0.3245$

    勝算比之95%信賴區間為
    $ e^{0.2303 \pm 1.96 \times 0.3245} \Rightarrow [ 1.500,2.378 ] $
    註：題2.3.需要個案數才能計算，若設定不同，結果也會不

※本站所有內容皆為志光教育科技集團版權所有，未經同意請勿任意複製、轉載、發行或刊他處。

▲
TOP