112高考衛生行政

生物統計學

申論題

擬答

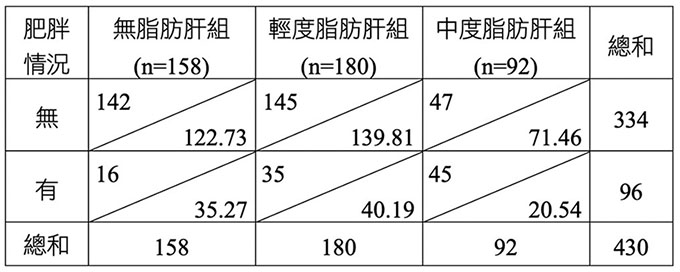
《題型解析》：本題結合了單母體平均數之信賴區間與雙母體平均差的假設檢定，因為試卷並無合適的t表，所以建議皆可採用大樣本Z分配的做法即可，111年高考二級衛技出了類似考題。
《命中特區》：生物統計學/王瑋｜志光出版，頁175～176；生物統計學精選500題全解/王瑋｜志光出版，頁199～200。
  1. 假設 X 代表吸菸組FEV1，Y代表非吸菸組FEV1 吸菸組FEV1平均值的95%信賴區間為
    $\bar{X} \pm Z_{0.025} \cfrac{ \sigma _x }{\sqrt{n}}$
    $\Rightarrow 3.3 \pm 1.96・\cfrac{ 0.68 }{\sqrt{224}}$
    $\Rightarrow [ 3.2109,3.3891]$
  2. $H_0:\mu_x= \mu_y$　　$H_1:\mu_x \ne \mu_y$
    $a = 0.05$
    $ Z^* $ $= \cfrac { \bar{X} - \bar{Y} }{ \sqrt{\cfrac{\sigma_x^2}{n_X} + \cfrac{\sigma_Y^2}{n_Y }}}$ $= \cfrac { 3.3 - 2.92 }{ \sqrt{\cfrac{0.68^2}{224} + \cfrac{0.71^2}{116}}}$

    $= 4.75\in C $

    $ C:\{ |Z^*｜> Z_{0.025} =1.96\}$


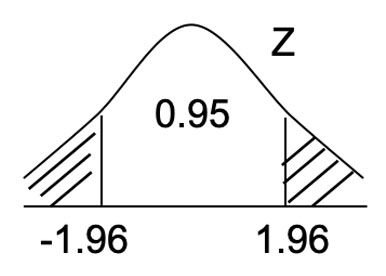
    拒絕 $H_0$，有顯著的證據說・
    兩組第一秒用力呼氣量平均值有差異
擬答

《題型解析》：本題結合了卡方獨立性檢定與雙母體比例差信賴區間，兩者皆為課內的基本內容，但早年很少結合兩者，而本題型式如同去年111年高考二級衛技試題，預期將來會是重要的考點。
《命中特區》：生物統計學精選500題全解/王瑋｜志光出版，頁330。
  1. 計算各格子的期望值$ E_{ij} = \cfrac{R_i \times C_j }{n} $，並將資料整理如下，並且斜線的左上方為觀察值，右下角為期望值：
    $H_0$ 有無肥胖與脂肪肝嚴重程度無關
    $H_1$ 有無肥胖與脂肪肝嚴重程度有關

    $a = 0.05$
    $df =(2-1) \times (3-1)=2$
    $ C:\{ X^{2*} > X_{0.05}^{2} (2)=5.99\}$


    $X^{2*} $ $=\sum \cfrac{(O_i - E_i)^2}{E_i}$ $ = \cfrac {(142-122.73)^2 }{122.73} + ... $ $ + \cfrac {(45-20.54)^2}{20.54} $ $ = 51.92 \in C $
    拒絕$H_0$ ，有顯著證據說有無肥胖與脂肪肝嚴重程度有關
  2. 中度脂肪肝組與無脂肪肝組肥胖比率差異的95%信賴區間為
    $ (\hat{p}_3 - \hat{p}_1) \pm $ $ Z_{0.025} \sqrt { \cfrac {\hat{p}_3 (1-\hat{p}_3)}{n_3} + \cfrac {\hat{p}_1 (1-\hat{p}_1)}{n_1} }$

    $\Rightarrow ( \cfrac{45}{92} - \cfrac{16}{158}) $ $ \pm 1.96 \sqrt{ \cfrac { \cfrac {45}{92}\times \cfrac {47}{92} }{92} + \cfrac { \cfrac{16}{158} \times \cfrac {142}{158} }{158}}$

    $\Rightarrow [ 0.2754, 0.5003]$
擬答

《題型解析》：單因子變異數分析是課內基本內容，但近年通常以填表為主，較少利用綜合統計量實際計算各種平方和，108年轉任衛行有類似考題。
《命中特區》：生物統計學/王瑋｜志光出版，頁203～206；生物統計學精選500題全解/王瑋｜志光出版，頁277～236。

假設1st組代表現在吸菸組，2nd為過去吸菸組，3rd組是從未吸菸組 已知
$ n_1 = 277$ ， $ \bar{X}_1. = 44.5 $ ， $s_1 = 11.1$
$ n_2 = 150$ ， $ \bar{X}_2.= 46.2 $ ， $s_2 = 13.6$
$ n_3 = 148$ ， $ \bar{X}_3. = 50.8 $ ， $s_3 = 12.9$

$ SST $ $ = \sum \sum (\bar{X}_i. - \bar{X}.. )^2$ $ = \sum n_i ( \bar{X}_i. - \bar{X}.. )^2 $ $ =3855.5874$

$ SSE $ $ = \sum \sum (X_ij - \bar{X}_i. )^2$ $ = \sum ( n_i -1 ) s_i^2 $ $ =(277-1) \times 11.2^2 + (150-1) \times 13.6^2 $ $+(148-1) \times 12.9^2 $ $= 86027.27$

$SSTO =SST + SSE = 89882.8574$
ANOVA表
 SSdfMSF
Treatment3855.587421927.793712.818
Error86027.27572150.3973 
Total89882.8574574 

$ H_0 : \mu_1 = \mu_2 = \mu_3 $ $ H_1 : \mu_i $不全相等
$ a=0.05 $
$ C : \{ F^* > F_{2,572,0.95} \thickapprox 3.83 \}$

$ F^* = 12.818 \in C $
拒絕 $ H_0 $，有顯著的證據說三組高密度脂蛋白膽固醇有差異。
註：本卷未附合適的F查表值
擬答

《題型解析》：課內已強調迴歸分析屬考試基本必出題，本題難度並不高，迴歸係數表與變異數分析表解讀，以及迴歸係數與判定係數的解釋本就是必考題，應可完整拿下分數。近年在111年高考衛行與111年地特三等衛生皆有類似考題。
《命中特區》：生物統計學/王瑋｜志光出版，頁300～301；生物統計學精選500題全解/王瑋｜志光出版，頁379～380與390～394。
  1. 設尿酸為$X_i$ ，血清肌酸酐為 $Y_i$
    線性迴歸方程式為
    $ \hat{Y} = 0.048 + 0.604X $
    代表每增加1 mg/dL尿酸，則血清肌酸酐增加0.604 mg/dL
  2. $ H_0 : \beta_1 = 0 $ $ H_1 : \beta_1 \ne 0 $
    $ a=0.05 $
    $ T^* = 9.337$ ，對應之 $ p - value < 0.001 < a = 0.05 $
    拒絕 $ H_0$，代表迴歸模式有達到統計上的顯著性
  3. 判定係數 $ R^2$ $ = \cfrac {SSR}{ SSTO } \times 100\%$ $=\cfrac {1.85}{10.61} $ $ = 17.44\% $
    代表以尿酸來預測血清肌酸酐有17.44%解釋度

※本站所有內容皆為志光教育科技集團版權所有，未經同意請勿任意複製、轉載、發行或刊他處。

▲
TOP